Компактификация/универсализация формальных описаний: нахождение аналогий в формулах
После критики эти догадки ещё и будут смешиваться с другими «догадками». Для этого находятся какие-то аналогии. Некоторые понятия и отношения между ними из разных теорий оказываются близкими, их отождествляют, а дальше работают с более компактной общей теорией. Есть множество подходов к тому, как находить аналогии и что такое вообще «рассуждение по аналогии», что такое вообще «аналогия». Самым популярным автором в этой области был Дуглас Хофштадтер, написавший «Гёдель, Эшер, Бах: эта бесконечная гирлянда» (1979)[1]. В математике поиск аналогий крайне популярен: теория категорий многими заявляется как хороший инструмент для отождествления находок в разных областях математики, а поскольку эти математические объекты представляют ещё и физические объекты, то можно говорить и об отождествлении находок в разных областях физики. Вот классическая работа на эту тему, с выразительным названием «Physics, Topology, Logic and Computation: A Rosetta Stone», 2009[2]. В физике диаграммы Фейнмана используются для рассуждений о квантовых процессах. В 1980-х годах стало ясно, что в основе этих диаграмм лежит мощная аналогия между квантовой физикой и топологией: а именно, линейный оператор ведёт себя очень похоже на «кобордизм»[3]. Подобные диаграммы можно использовать для рассуждений о логике, где они представляют доказательства, и вычислениях, где они представляют программы. С ростом интереса к квантовой криптографии и квантовым вычислениям стало ясно, что существует обширная сеть аналогий между физикой, топологией, логикой и вычислениями. В работе «Розеттский камень» Joan Baez и Mike Stay уточняют некоторые из этих аналогий, используя понятие «замкнутой симметричной моноидальной категории»[4]. После описания взаимодействия систем как процессов в сетях/networks (электрические, гидравлические сети, а также сети взаимодействий в системной динамике, обычно связываемые с функциональными представлениями системы, то есть представлениями времени функционирования) Joan Baez делает предложение об использовании формализма теории симметричных моноидальных категорий для описания не просто процессов, но открытых систем, подразумевающих взаимодействие с окружающей средой[5]. Опять мы видим ход на использование теории категорий как foundational ontology для онтологии системы, и основной ход — это переход от выражения онтологии в статичных отношениях к морфизмам, изменениям. Этот ход соответствует ходу на конструктивизм в математике, когда от "вечных классов"/eternal classes и их отношений мы переходим к операциям построения/construction[6].
Коннективистскую/распределённую/интуитивную линию рассуждений (реализуемую сегодня нейросетями) представляет работа с переводами: «аналогия между двумя текстами об одном и том же на разных языках». Берём множество объектов и отношений из огромного набора (корпуса) текстов какого-то языка о нашем мире и сопоставляем его с теми же объектами и отношениями корпуса текстов о нашем же мире на другом языке. Языковые модели в форме предобученных на корпусе текстов нейронных сетей ровно это и делают: берут два облака точек «описания мира» на двух языках (на самом деле — на сотне языков, далее в картинках, далее в действиях людей и роботов, далее в аудио, и т.д.) в многомерном пространстве смыслов и как-то совмещают их друг с другом так, чтобы по возможности направления в этом пространстве соответствовали отношениям — и максимально совмещают их «точка в точку», при этом точки в пространстве смыслов представляют собой понятия, а вот направления векторов характеризуют отношения между понятиями.
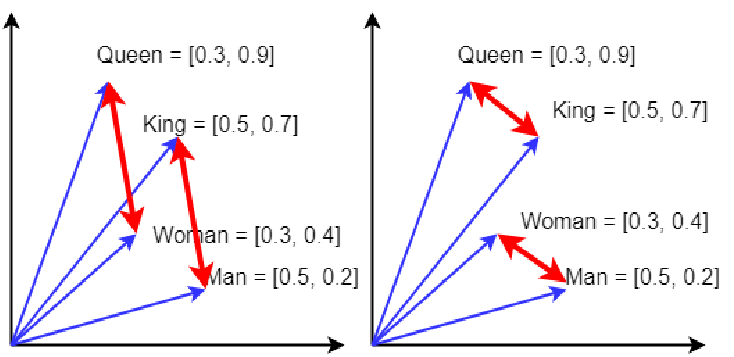
Это грубая модель, но современные нейросетевые модели переводят тексты, включая перевод на язык, на котором нет параллельных текстов[7], в том числе работая не только нейролингвистически (текстами), но и мультимодально (картинки и т.д.): используется тот факт, что описываем-то в корпусах текстов, картинках, объектах для «ощупывания» в действиях робота один и тот же мир[8]. Проблема в том, что точность такого перевода заведомо оценить нельзя, а если переводить несколько раз, то будет эффект «испорченного телефона» (каждый раз вроде как вносится небольшая ошибка, но через три-четыре перевода результат вообще оказывается непохож на оригинал).
Эти проблемы легко преодолеваются, если опираться не на быстрое интуитивное «нейросетевое» аналоговое мышление S1, но на медленное и трудозатратное логическое мышление S2, которое весьма эффективно реализуется классическими электронными компьютерами, и которое реализуется эмуляцией «логического вычислителя» на нейросетевых вычислителях, в том числе человеческом мозге. В развитии цивилизации должна присутствовать строгость и краткость описания мира, это и даёт математика. Человечество опирается в своём познании и изменении мира в том числе на символистскую, а не только на коннективистскую онтологическую работу/метамоделирование. Символическая/семиотическая работа идёт на высоком уровне формальности/строгости/изученности поведения объектов, то есть задействует математику.
Наука достигла сегодняшнего состояния как раз за счёт использования математики как мета-мета-мета-модели**/foundationmodel** для онтологии своих поднаук**, то есть наука опиралась на структурное сходство рассуждений по** формулам для разных объектов внимания. Это и есть основной путь науки. При этом в математике есть ещё и предпочтения: примат булевой логики и полной формальности над байесовскими вероятностными вычислениями с их неопределённостью и квантовыми вычислениями с их ещё большими неопределённостями. Одна беда: чем более формальны описания (длиннее цепочка присвоения типов**,** то есть прописаны все типы по линии M0-M3 и иногда и M4**, да ещё и для точности введены промежуточные уровни****), тем больше нужно умственных усилий и тренинга для удержания этой цепочки. Поэтому большинство населения работает с онтиками, используя интуитивное** нестрогое присвоение типов и неформальные (квантовоподобные, даже не байесовские, как это выясняется в современных исследованиях по теории принятия решений) правила рассуждений над типами M3 и M4, а хорошо обученное меньшинство населения (учёные) ухитряются работать со всей цепочкой, выдерживая строгую/булеву логику рассуждений с формальными типами на высоких уровнях абстракции**—** в том числе снимая неминуемые противоречия, возникающие на этих уровнях абстракции при попытке объединять рассуждения по разным онтикам**.**
Противоречия неминуемо проскакивают в этот мир строгой формализации, если используются разные онтики. Формализация имеет образовательный ценз, физмат-моделирование (моделирование явлений физического мира средствами математики) доступно не всем, ему нужно учить специально так же, как любой другой работе с типами: учить как набору лучших имеющихся типов как типов объектов внимания в какой-то предметной области, так и операциям присвоения типов и проверки, насколько удачны были догадки об этих типах (критика логическая и экспериментальная). И ещё есть ресурсный ценз на альтернативную формализацию отдельных онтик каждый раз, когда будет найдено очередное противоречие, возникающее при попытке общего описания. Даже у учёных с их компьютерами может просто не хватать ресурсов для ведения строгих рассуждений, требующих упоминания объектов из разных предметных областей.
Ситуация ещё сложнее в силу запутанности конечных классификаций/присвоений типа в классификационной иерархии как отношения репрезентации между физическим миром и абстрактным/математическим миром и наличием функциональных (в каком-то смысле "идеальных", обобщённых, типизирующих, ролевых) объектов, в которых выполняется моделирование физического мира. Объекты из учебника физики проще считать функциональными (рассматриваемыми в run-time) с их репрезентацией абстрактными/математическими объектами с хорошо изученным в математике поведением, а вот продукты/модули/конструктивные объекты какого-то прикладного domain — это уже физические объекты (а не объекты из учебника физики, те как раз функциональные!). То есть помидоры на весах мы моделируем как помидоры::продукт/физический объект, реализованный/realized/implemented by физическое тело::функциональный_объект, описываемый весом::переменная::скаляр::абстрактный/математический объект. Иначе не разобраться, см., например рассуждения по поводу понимания концепта Markov blanket у разных авторов у Ian Glendinning[9].
Этот подход «совмещения формальных описаний» на базе сходства отношений между объектами этих описаний обычен и в мире «промышленных» онтологий, где вместо математической upper ontology с формулами, как у физиков, используется только foundational ontology из логики. John Sowa в софте компании VivоMind реализовал подход VAE (VivoMind Analogy Engine), когда просто ищутся два фрагмента графа знаний с одинаковой структурой объектов и отношений, такое даже компьютеру можно поручить (и в работах VivoMind показывается, что такой подход вполне практичен, есть успешные приложения AI, полученные во времена, когда ещё не было нейросетей)[10]. И таких работ множество, хотя тот же John Sowa после многих лет мучений с таким подходом пишет, что подобные методы поиска аналогий в правой/строгой части спектра формальности мышления очень вычислительно трудоёмки и вскрывают проблему: никакие промышленные upper ontologies не помогают в поисках аналогий, для разных задач удобные для них мета-мета-мета-модели кардинально различаются и общих рассуждений по ним принципиально не построишь.
Аналогичный результат будет и для вероятностных описаний: общее байесовское рассуждение для разных статистических теорий не проведёшь, приходится переходить к квантовоподобным, то есть переносу математики, разработанной для квантовой механики, на другие предметные области. Это требует перехода от колмогоровской теории вероятностей для вычислений по Байесу, которые в какой-то степени соответствуют строгой булевой алгебре, ко множеству несовместимых вероятностных алгебр, что отмечает в своих работах Андрей Хренников[11]. Отказ от «булевости» и «байесовоскости» важен также для более ресурсно-адекватного моделирования мира и отмечается также и другими авторами (квантовоподобные представления линейны и дискретны, это резко уменьшает объем вычислений, кроме того «байес» откидывает вероятности априорных событий, о которых мы не знаем, а квантовоподобный расчёт как-то их учитывает)[12].
В функциональных объяснительных теориях ищут одинаковую структуру математических формул, которыми они выражены (при этом смотрят на то, чтобы речь шла не об одной формуле, а о каком-то массиве формул, чтобы подобие было более-менее развёрнутым/очевидным, а не эпизодическим случайным совпадением)****— и делают выводы, что природа хорошо описываемых одинаковыми формулами явлений похожа, это всё проявления каких-то общих закономерностей**.** Каждый такой случай закрепляет использование общего для многих случаев математического аппарата. Ровно таким образом распространились классические «исчисления», а в последнее время распространяется «новый треугольник», просто предлагаемые ими математические объекты оказались очень универсальными в плане возможностей описания физического мира.
https://en.wikipedia.org/wiki/Symmetric_monoidal_category, https://en.wikipedia.org/wiki/Closed_monoidal_category ↩︎
Symmetric Monoidal Categories: a Rosetta Stone, https://johncarlosbaez.wordpress.com/2021/05/28/symmetric-monoidal-categories-a-rosetta-stone/ ↩︎
Constructive Mathematics, https://plato.stanford.edu/entries/mathematics-constructive/ ↩︎
https://mt.cs.upc.edu/2021/02/08/major-breakthroughs-in-multilingual-neural-machine-translation-ii/ ↩︎
https://www.sciencedirect.com/science/article/pii/S0303264720301994 и https://www.frontiersin.org/articles/10.3389/fnbot.2022.910161/full#B45 ↩︎